Physical History
Exponential functions
By Mark Ciotola
First published on May 17, 2019. Last updated on February 6, 2021.
Introduction
Functions
Functions relate at least one variable to at least one other number or variable. is a variable. Its value could be anything. Yet, consider the equation:
\(x = 1\)
Here, x is constrained to equal to a single particular number, which is 1. Such a number is known as a constant. It’s value in the equation cannot change. Things get more interesting when a variable is related to another variable. For example, let’s say that
\(y = 2x\).
Both x and y are variables. However, the value of either variable can change, depending on the value of the other variable. Below are some sample pairs of values allowed by this equation:
| x | y |
|---|---|
| -2 | -4 |
| -1 | -2 |
| 0 | 0 |
| 1 | 2 |
| 2 | 4 |
| 10 | 20 |
Such a function acts as a constraint of the values. If x is 1, then y must be 2.
Functions can take many forms, such as y = x^3, z = 2x + 5y, or y = sin x, where sin is shorthand for the trigonometric function sine, what can be expressed quantitatively as a series of numbers.
What Exponential Functions Are
Exponential functions are functions where a constant is raised to a power. For example,
\(y = 7^x\).
Here, the values of x and y are:
| x | y |
|---|---|
| -2 | 1/49 |
| -1 | 1/7 |
| 0 | 1 |
| 1 | 7 |
| 2 | 49 |
| 3 | 343 |
You can see that exponential functions can increase very quickly. There is a very special constant called equal to 2.71828. e is a very special number in mathematics for many reasons. However, it is also a very useful base for exponential functions. e is typically used as the base for exponential functions.
Pure exponential growth
Pure exponential growth is that which is proportional to its current quantity. In principle, a system that is capable of self-replication can experience pure exponential growth.
It can apply to populations of bacteria, fish and even humans. It can apply to chain reactions in nuclear physics as well.
Bacteria (photo credit: CDC US government)
Humans can self-replicate, so human societies can also experience pure exponential growth, in the form of y = et, where the value of e is approximately 2.72.
Pure exponential growth begins slowly, then literally explodes over time. Sometimes the plot of exponential growth is described as a “hockey stick” because it starts nearly horizontally, then “turns the corner” and grows nearly vertically.
It typically concerts population differential equations such as
\(\frac{dP}{dt} = kP\).
where P is population, t is time and k is a proportionality constant. The solution for this equation is the classic exponential growth function
\(P = P_0 e^{kt}\).
where is the initial population.
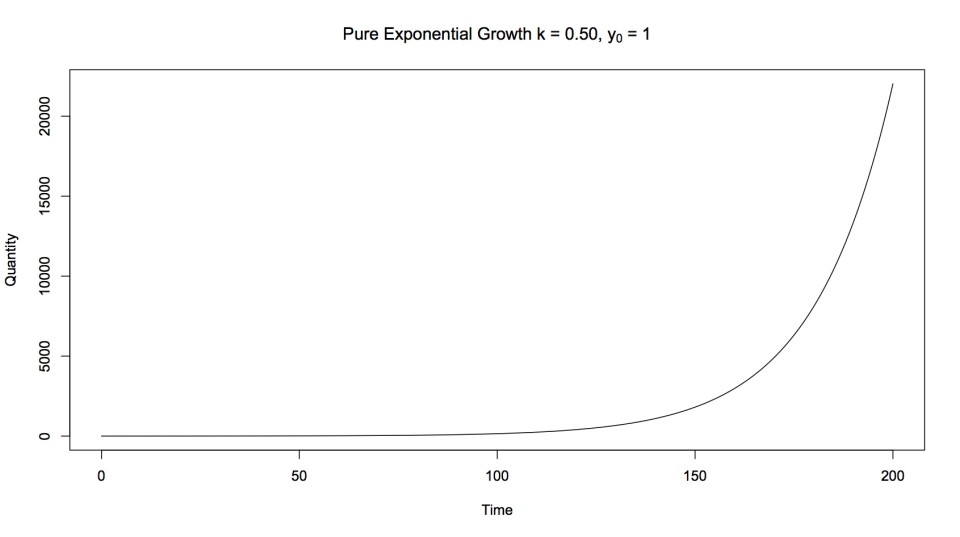
Pure exponential growth
Different growth rates result in different levels of growth at a particular point of time, but growth is still ultimately explosive (see below).
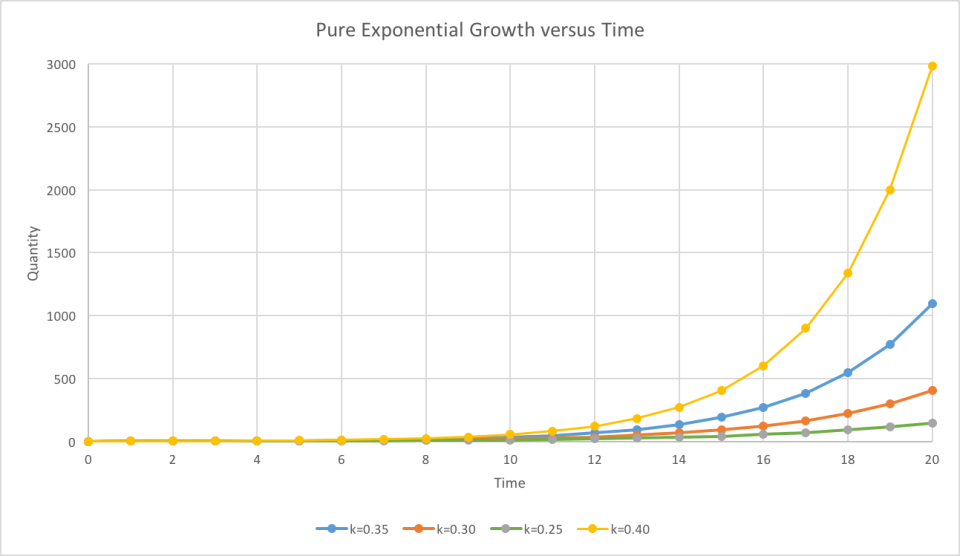
Pure exponential growth for different growth rates
Human social movements can also experience exponential growth. Many philosophies have been subject to exponential growth, because the founder could teach others to teach yet others. Investment pyramid schemes can also experience exponential growth.
Certain types of growth not only grow, but cause changes in their environment to enable further growth.
Some futurists make dire projections of explosive population growth and resource consumption by extending a pure exponential function into the future.[2]In reality, exponential growth is never seen for long periods of time, due to limiting factors.
It is noticed that systems in both nature and human society often grow exponentially at times (Ciotola 2001; Annila 2010). Exponential growth essentially means that a system’s present growth is proportional to its present magnitude. For example, if a doubling of population (say of mice) is involved, then 10 mice will become 20 mice, while 20 mice will become 40 mice. A formula for exponential growth is:
\(y = ek^t\)
where \(y\) is the output, \(k\) is the growth rate, and \(t\) represents time.
Logistic Growth
A resource that is renewable, but limited in the short-run, can be modeled with a logistics curve. Examples of such resources are new-growth forests and wild Pacific salmon. They can be nearly totally consumed in the short run, but these resources can restore themselves if they have not been exploited too completely. A logistics curve is not shown here, but is in the shape of an elongated “S” and can be found in many differential equations textbooks. The beginning (and bottom) of the “S” represents the initial exploitation. The forward-sloping “back” of the “S” represents nearly pure exponential growth. The end and top of the “S” represents a leveling off of growth, as consumption of the resource matches its ability to restore itself.
In logistic growth, population tends to move towards a particular population level that reflects the carrying capacity of the system or environment. Such functions are also called S-curves.
Logistics functions are in the form of:
\(\frac{dP}{dt}=k (1-\frac{P}{N})P\),
where P is population, t is time, k is a growth rate coefficient and N is the carrying capacity. N can also be viewed as the periodic replenishment of potential.
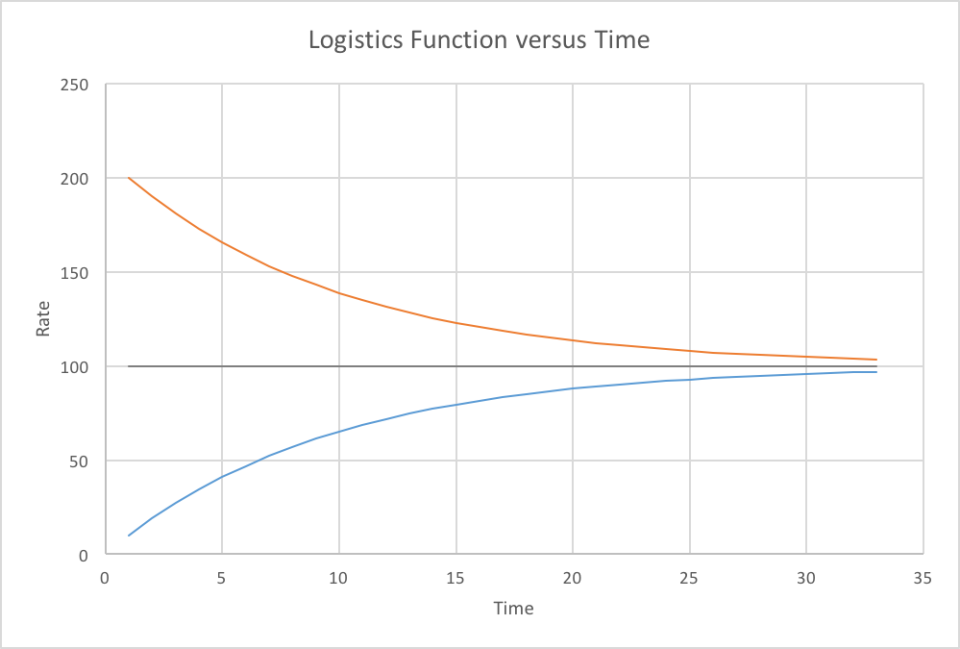
Logistic growth
Achieving a logistics curve is the holy grail of sustainability enthusiasts. Applying concepts of sustainability to an entire dynasty or regime is called Big Sustainability, and involves social and economic sustainability, as well as physical resource sustainability (e.g. sufficient desired resources and ability to avoid toxins).
Decay
Exponential decay of efficiency is produced by a Carnot engine operating across an exhaustible thermodynamic potential. It is a fundamental form of decay. The following is an equation for an exponential decay function:
\(y = e^{-k^t}\) ,
where \(k\) is the decay factor. This appears nearly identical to the exponential growth function, except that the exponent is negative.
Efficiency-Discounted Exponential Growth
Efficiency-Discounted Exponential Growth (EDEG) involves the consumption of a non-replenished resource over time by a system of reproducing agents. It can be useful for modeling mineral production of a mining region.
The efficiency-discounted exponential growth (EDEG) approach is relatively new, although functions similar in output have existed for over 100 years. A few rough simulations were conducted earlier (Ciotola 2009, 2010), but this approach is being further refined and structured. EDEG produces a model based on two mathematically simple components, but allows the addition of other, more sophisticated components.
This author’s original efforts at developing the EDEG approach were heavily influenced by M. King Hubbert, a geologist who used such curves to model domestic petroleum production (including peak oil) as well as labor model.[7] Hubbert in turn was influenced by D. F. Hewett.
It is possible to create differential equations that produce EDEG. It is also possible to empirically synthesize functions that closely replicate EDEG. An analytical solution to EDEG differential equations from fundamental principles has not yet been created. However, the differential equations can be iteratively calculated via a spreadsheet or computer program to produce useful results.
The author originally used the normal distribution approach (Ciotola, 2001) discussed by Hubbert, but this approach was not sufficiently broad for the authors need to model history, since few historical dynasties utilized petroleum in major quantities, nor did Hubbert’s attempts involve a driving tendency for history. The author began some related models for French and Spanish dynasties (2009) and more fully developed EDEG for petroleum modeling (Ciotola 2010).
It is not yet possible to analytically create a EDEG function from fundamental principles. However, EDEG can be expressed as a differential equation, which can then be iteratively calculated via a spreadsheet or computer program.
When developing an EDEG model, an effort should be made to express parameters in terms of a potential and changing efficiency. If the quantity of the most critical conserved resource is known, then the model for total consumption over time should match that quantity.
An EDEG function can be approximated by multiplying a pure exponential growth function by an efficiency function:
\(P = k_1 e^{k_2 t} (1 – \frac{Q}{Q_h})\),
where P is power (or production), is a constant of proportionality, typically the initial prediction (or power), is a growth factor, is the amount of a nonrenewable critical resource thus far consumed, and is the initial quantity of the nonrenewable critical resource.
represents the exponential growth component.”
\((1 – \frac{Q}{Q_0})\)
represents the efficiency component.
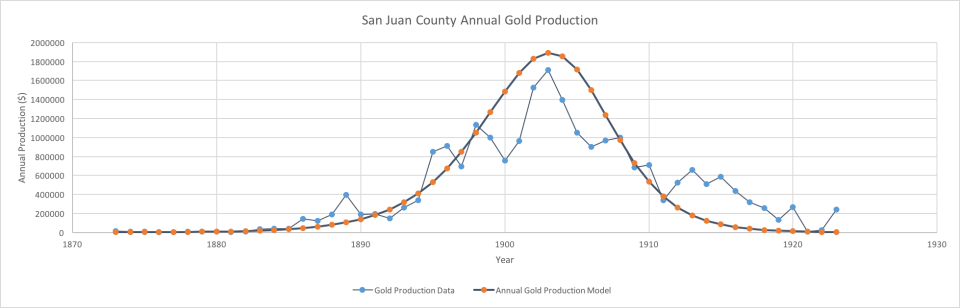
Colorado San Juans gold production versus model
HS Curves
It may also be possible to create a function that transforms an H-Curve (EDEG) to an S curve. There is an initial amount of a non-renewable critical resource, and then periodic replenishment of that resource.”
Efficiency Discounted-Exponential Growth (EDEG) Approach
The efficiency-discounted exponential growth (EDEG) approach is relatively new, although functions similar in output have existed for over 100 years. A few rough simulations were conducted earlier (Ciotola 2009, 2010), but this approach is being further refined and structured. EDEG produces a model based on two mathematically simple components, but allows the addition of other, more sophisticated components.
Origins of This Approach
This author’s original efforts at developing the EDEG approach were heavily influenced by M. King Hubbert, a geologist who used such curves to model domestic petroleum production (including peak oil) as well as labor model.[7] Hubbert in turn was influenced by D. F. Hewett.
The author originally used the normal distribution approach (Ciotola, 2001) discussed by Hubbert, but this approach was not sufficiently broad for the authors need to model history, since few historical dynasties utilized petroleum in major quantities, nor did Hubbert’s attempts involve a driving tendency for history. The author began some related models for French and Spanish dynasties (2009) and more fully developed EDEG for petroleum modeling (Ciotola 2010).
Exponential Growth
In principle, a system that is capable of self-replication can experience pure exponential growth. Examples include bacteria, fire and certain nuclear reactions. Humans can self-replicate, so human societies can also experience pure exponential growth, in the form of y = et, where the value of e is approximately 2.72. An example of pure exponential growth is graphed below.

Human social movements can also experience exponential growth. Many philosophies have been subject to exponential growth, because the founder could teach others to teach yet others. Investment pyramid schemes can also experience exponential growth.
Certain types of growth not only grow, but cause changes in their environment to enable further growth.
Some futurists make dire projections of explosive population growth and resource consumption by extending a pure exponential function into the future.[2]In reality, exponential growth is never seen for long periods of time, due to limiting factors.
It is noticed that systems in both nature and human society often grow exponentially at times (Ciotola 2001; Annila 2010). Exponential growth essentially means that a system’s present growth is proportional to its present magnitude. For example, if a doubling of population (say of mice) is involved, then 10 mice will become 20 mice, while 20 mice will become 40 mice. A formula for exponential growth is:
\(y = ek^t\)
where \(y\) is the output, \(k\) is the growth rate, and \(t\) represents time.
Efficiency-Discounted Exponential Growth
Efficiency-Discounted Exponential Growth (EDEG) involves the consumption of a non-replenished resource over time by a system of reproducing agents. It can be useful for modeling many phenomena, including the mineral production of a mining region.
It is possible to create differential equations that produce EDEG. It is also possible to empirically synthesize functions that closely replicate EDEG. An analytical solution to EDEG differential equations from fundamental principles has not yet been created. However, the differential equations can be iteratively calculated via a spreadsheet or computer program to produce useful results.
When developing an EDEG model, an effort should be made to express parameters in terms of a potential and changing efficiency. If the quantity of the most critical conserved resource is known, then the model for total consumption over time should match that quantity.
An EDEG function can be approximated by multiplying a pure exponential growth function by an efficiency function.
\(P = k_1 e^{k_2 t} (1 – \frac{Q}{Q_0})\),
where P is power (or production), \(k_1\) is a constant of proportionality, typically the initial prediction (or power), \(k_2\) is a growth factor, \(Q\) is the amount of a nonrenewable critical resource thus far consumed, and \(Q_0\) is the initial quantity of the nonrenewable critical resource.
\(k_1 e^{k_2 t}\)
represents the exponential growth component.
\((1 – \frac{Q}{Q_0})\)
represents the efficiency component.

Colorado San Juans gold production versus model
Notes and References
[1] Meadows, et al. makes this point in Limits to Growth.
[2] For an opposing, but still dire view, see D. H. Meadows et al, Limits to Growth, Universe Books, New York (1972).
[3] The work of Forrester on system dynamics and the Club of Rome project Limits to Growthby Meadows et al involve attempts to better understand these limiting factors. The work of M. K. Hubbert and Howard Scott on peak oil and technocratic governance are other examples.
[4] M. Butler, Animal Cell Culture and Technology. Oxford: IRL Press at Oxford University Press, 1996.
[5] Ciotola, M. 1997. San Juan Mining Region Case Study: Application of Maxwell-Boltzmann Distribution Function. Journal of Physical History and Economics 1. Also see M. K. Hubbert.
[6] Heilbroner, R. L., The Worldly Philosophers 5thEd. (Touchstone (Simon and Schuster), 1980.
[7] Such curves were proposed by W. Hewitt as early as 1926 (source unavailable).
[8] See Gibson, C., Spain in America. Harper and Row, 1966.
Additional References
Annila, A. and S. Salthe. 2010. Physical foundations of evolutionary theory. J. Non-Equilib. Thermodyn. 35:301–321.
Ciotola, M. 2001. Factors Affecting Calculation of L, edited by S. Kingsley and R. Bhathal. Conference Proceedings, International Society for Optical Engineering (SPIE) Vol. 4273.
Ciotola, M. 2003. Physical History and Economics. San Francisco: Pavilion Press.
Ciotola, M. 2009. Physical History and Economics, 2nd Edition. San Francisco: Pavilion of Research & Commerce.
Ciotola, M. 2010. Modeling US Petroleum Production Using Standard and Discounted Exponential Growth Approaches.
Hewett, D. F. 1929. Cycles in Metal Production, Technical Publication 183. New York: The American Institute of Mining and Metallurgical Engineers.
M. King Hubbert. 1956. Nuclear Energy And The Fossil Fuels. Houston, TX: Shell Development Company, Publication 95.
Hubbert, M. K. 1980. “Techniques of Prediction as Applied to the Production of Oil and Gas.” Presented to a symposium of the U.S. Department of Commerce, Washington, D.C., June 18-20.
Mazour, A. G., and J. M. Peoples. 1975. Men and Nations, A World History, 3rd Ed. New York: Harcourt, Brace, Jovanovich.
Schroeder, D. V. 2000. Introduction to Thermal Physics. San Francisco: Addison Wesley Longman.
Smith, D. A. 1982. Song of the Drill and Hammer: The Colorado San Juans, 1860–1914. Colorado School of Mines Press.