Thermodynamic Expression of Economics
Expressing Supply and Demand Thermodynamically
By Mark Ciotola
First published on May 17, 2019. Last updated on May 12, 2021.
Recall Fourier’s Law of Conduction
Recall the example of a thermal conductor operating upon exhaustible, nonrenewable reservoirs.
This is analogous to bridging market supply with demand. The hot reservoir has thermal energy to spare, and the cold reservoir wants some of that energy. So then, the hot reservoir has a supply function and the cold reservoir has a demand function.
The cold reservoir really “wants” that first bit of thermal energy a lot due the the high temperature difference! So it is willing to pay a high “price” for it. However, it wants each next bit of energy less and less, as its thermodynamic “hunger” becomes satisfied. Hence, demand slopes downward, just as the temperature difference does.
Eventually the two temperatures become equal, which is analogous to having satisfied all of the customer demand. This is shown in the thermodynamic supply and demand plot shown below.
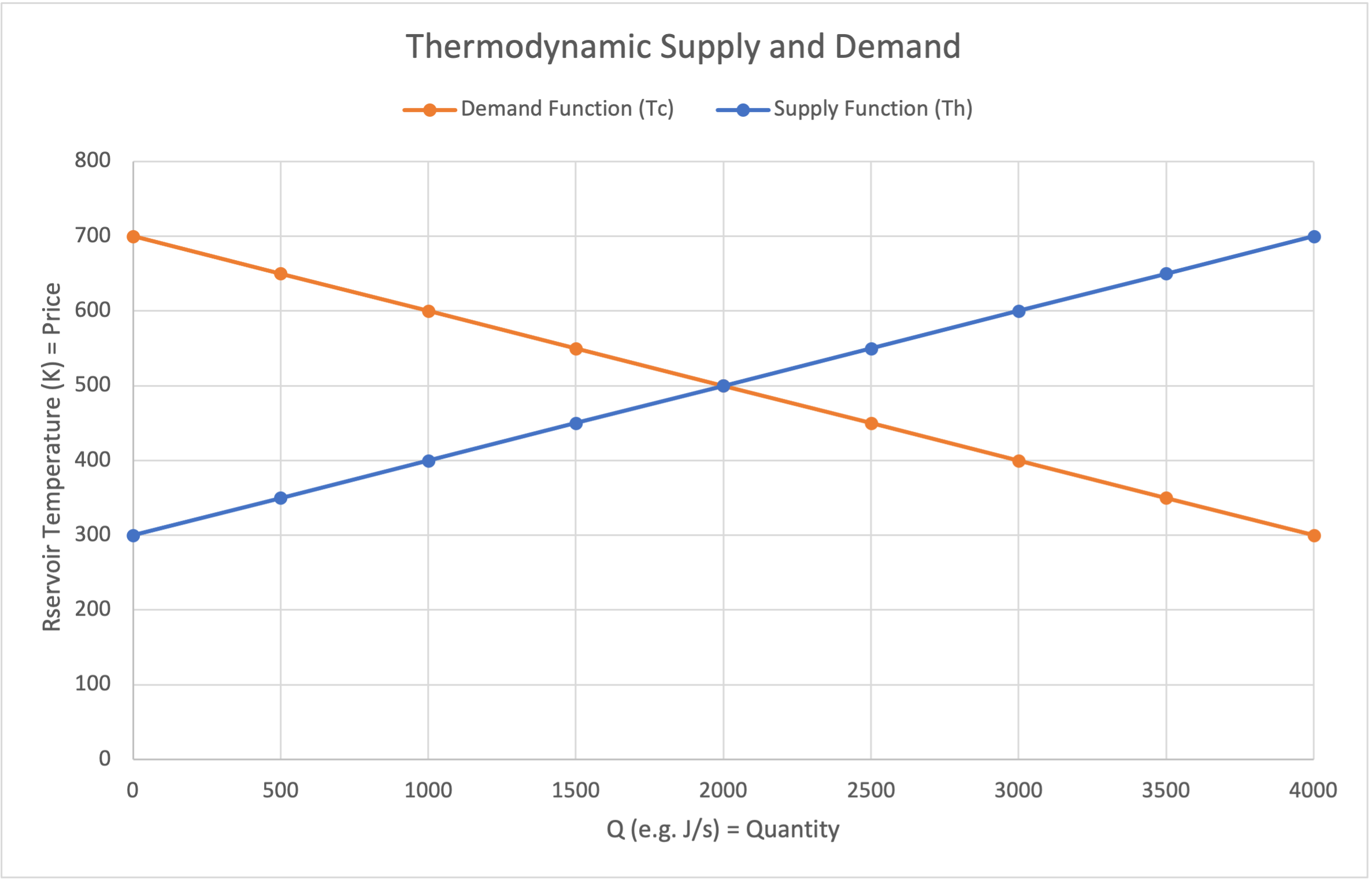
Thermodynamic expression of supply and demand
Per Fourier’s Law, the flow of thermal energy is shown at the intersection of the function plots. The temperature of the intersection will be that of an intermediary point on the conductor.
Market Price Equilibrium
Where there are both continuous sources of supply and demand, the market will eventually reach a market equilibrium where these two curves meet. Since such requires a continual flow of goods, this can be said to have reached dynamic equilibrium.
Sales Volume
Even at equilibrium, what is the sales volume? From where the supply and demand curves meet, we know the quantity transferred. For example, if the heat capacity of the hot reservoir is 1, and the temperature difference is 200 K, then there are 200 J of heat that can be spread around. Since these are, limited exhaustible reservoirs, their temperature increases when they receive heat and it decreases when they lose heat. Since the reservoir have an equal heat capacity, transferring 100 J of thermal energy will reduce the hot reservoir temperature by 100K and increase the cold reservoir temperature by 100 J, in which case they shall be of equal temperature (400K) and their “hot” hot “cold” labels will have become meaningless. This thermodynamic equilibrium is analogous to market equilibrium.
Note that the equilibrium price and quantity will be different for different reservoir characteristics, just as different suppliers and customers each how their own differing characteristics. Also, if the reservoirs are inexhaustible so that their temperature never changes, heat will flow, and their is a equilibrium quantity (called dynamic equilibrium), but the equilibrium temperature would have a different meaning in this context.